Hi Bob, Lynn
I agree with your assessments - doesn't make any sense otherwise.
There was a very smart individual I knew by name of Vance Jaqua.
I had several exchanges with him about propellers that made more sense to me
than what I read in Prop theory. I mean he really made sense about props
as it relates to the real and theoretical world. One of things he pointed
out regarding static thrust - was how crucial prop loading was to thrust
produced/ per horse power at/near static conditions. He took on some of
the basic tenants of current prop theory and pointed out some thinking that
just didn’t seem to make sense in the real world. Here is an
extract out of his “thinking paper” on propellers he shared with me
(my comments in blue)
The mass that we are going to accelerate for a classic
airplane propeller, is roughly a sort of cylinder of air the size of which is
related to the diameter of the prop. (in other words, whatever we do and however efficient it is or is not –
it’s all relative to this cylinder of air which is related to the
diameter of the prop – so the diameter of the prop appears to sort of set
a foundation element for all else)
The size of that cylinder of air controls the amount of
weight flow through the prop disk (That all important M(Mass) in our thrust and power calculations that we
discussed above). Now using that MV (momentum
= mass * velocity)formula, we can get 100 pounds force of thrust by
either accelerating 1 unit of mass by 100 feet per second, or by accelerating
100 units of mass by 1 foot per second, (or any other combination for which the
answer is 100).
However, remember the expression for power - M times
velocity squared, divided by two. This puts a big difference on how much power
we need to make the force. The 100 feet per second case computes to 5,000 ft
pounds of energy, where the 1 foot per second case is only 50 foot pounds. This
is for the static thrust case, and explains why helicopters and STOL type
airplanes use those big, rather slow turning propellers to get off the ground.
(this also helps explains why my going from a faster turning (68x72)
prop using the 2.17 gear box to a slower turning larger diameter (74x88) prop
using the 2.85 gear box increased my static thrust and take off
performance – it gave lighter disc loading)
As the airplane flies faster, the need for those large
diameters becomes less important, because now your disk is "running
into" lots of pounds per second just because of your forward velocity.
I thought these few words of Vance explained more to me than
an entire book of theory on props.
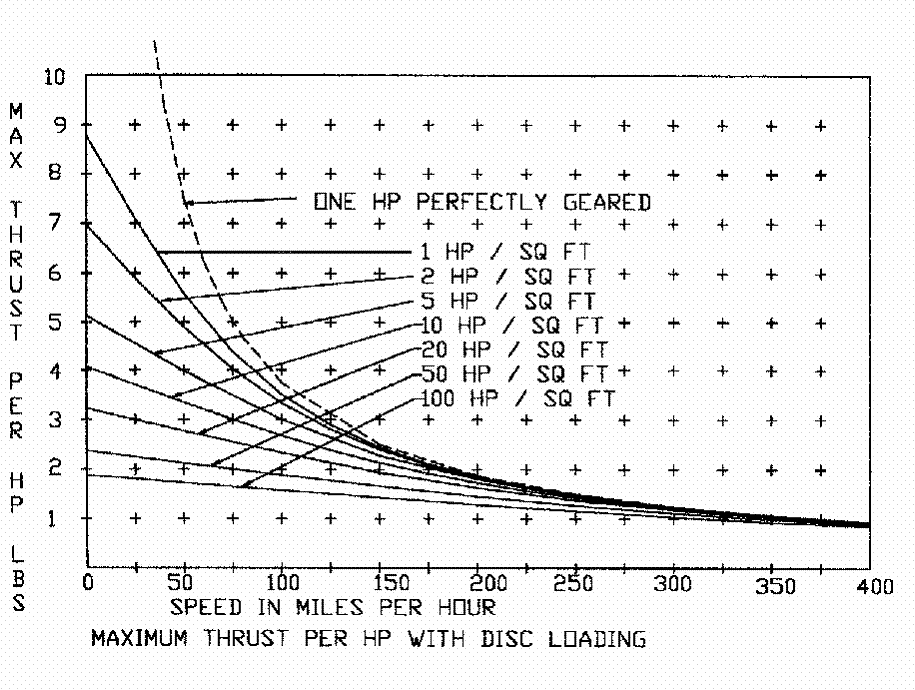
Here is a chart that Vance provided that illustrates
his point about low disc loading contributed to more static thrust. Particularly
note the difference it makes at zero airspeed (our static condition). A
very lightly loaded prop of 1 Hp /sq ft produces around 9 lbs of thrust per HP
at static whereas the higher loaded (more HP per sq ft of prop disc area) the
prop is - the less static thrust produced.
This might seem counter intuitive but Vance points out a
helicopter might have a disc loading as light as 0.25 Hp/sq ft. A helicopter can
clearly produce great amounts of static thrust as it lifts its own weight
vertically off the ground at “zero” airspeed. It would appear
that greater power and smaller prop produces less thrust due to the fact that a
smaller diameter blade is likely highly pitched to absorb the greater power and
likely has a large portion of its blade stalled or otherwise turbulent,
distorted air flow as the powerful engine churns the air. Even the book
theory indicates a slower turning prop is more efficient in using power to move
air.
Unfortunately, to the best of my knowledge, Vance never turned
his notes into a finished paper. He certainly had a viewpoint that I
found understandable.
Ed
Ed Anderson
Rv-6A N494BW Rotary Powered
Matthews, NC
eanderson@carolina.rr.com
http://www.andersonee.com
http://www.dmack.net/mazda/index.html
http://www.flyrotary.com/
http://members.cox.net/rogersda/rotary/configs.htm#N494BW
http://www.rotaryaviation.com/Rotorhead%20Truth.htm