|
I agree with your explanation, Bernie - but
not totally with your first assertion.
I agree that the pressure is due to the average
number of molecules striking a surface per unit time. A clearer explanation
than I had given. However, when an airmass is moving there is a
small translational velocity component (small compared to the molecule's nominal
velocity), imparted to the molecule (else it would not move in that
direction). This translational velocity component increases where the duct
narrows which as you stated, reduces the time available for molecules to
impact the wall resulting in fewer impacts per unit time => less
pressure. The opposite when the duct widens.
So the molecules total velocity magnitude IS
affected (even if minutely) by the translational velocity of the air.
This, of course, also explains what happens in the Bernoulli tube where the air
density is considered "incompressible" or non changing.
Below is an explanation I found which explains (I
believe) , that although often ignored for simplicity, air movement does impart
a translational component to the molecules velocity.
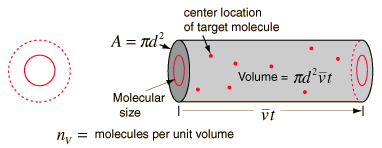
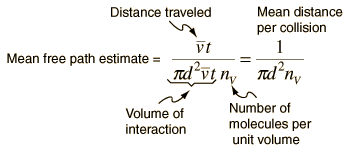
Mean Free Path
The mean free path or average distance between
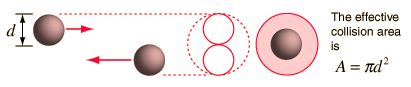
collisions for a gas molecule may be estimated from kinetic theory. Serway's approach is a good
visualization - if the molecules have diameter d, then the effective
cross-section for collision can be modeled by

using a circle of diameter 2d to represent a
molecule's effective collision area while treating the "target" molecules as
point masses. In time t, the circle would sweep out the volume shown and the
number of collisions can be estimated from the number of gas molecules that were
in that volume.
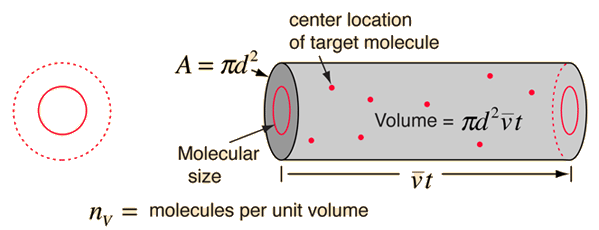
The mean free path could then be taken as the length
of the path divided by the number of collisions.
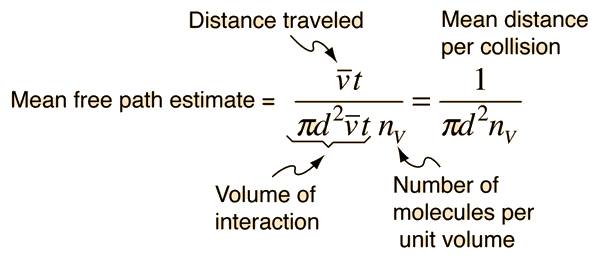
The problem with this expression is that the
average molecular velocity is used, but the target
molecules are also moving. The frequency of collisions
depends upon the average relative velocity of the randomly moving molecules.
I highlighted the words for emphasis but they are
as presented on the webpage which you can check at.
This shows (in my opinion) that pressure is
indeed affected by the average relative velocity component of the molecules
velocity as well as its velocity attributed to temperature. While the
translational component is quite small compared to the molecules velocity, it
does have an effect on pressure. No translational velocity component =>
no change in pressure. Since as you point out there is negligible
temperature change and therefore negligible change in the molecules "inherent"
velocity, the changes in pressure must be due to the difference in the
translational velocity component affects on the molecule.
Whew, I think I want to get back to work on
my digital flow meter.
Boy, isn't this fun. I wonder how we can use
it to abate Bernie's noise problem. It appears simply, Bernie, if you can
get your translational speed up past the average molecular velocity the noise
should no longer be a problem {:>)
Best Regards
Ed
----- Original Message -----
Sent: Monday, April 04, 2005 8:26 AM
Subject: [FlyRotary] Re: molecular movement Re:
Cooling -Learned a lot
>
> OK, I can't keep my blabber mouth shut on this subject any
longer.
>
> molecular velocity is only a function of the
temperature which is not changing in the diffuser. colder air has less molecular
velocity.
>
> The stagnation, pitot, total, dynamic pressure (Pt)
does not change if we have a friction free wall. Why does the static
pressure (P) along the wall go up as we slow the air down? If Pt is not changing
and velocity is decreasing then the Bernoulli equation lets us calculate the P
value. We can ignore the small density change in our low velocity arena. One way
to think of this is that the P is proportional to the number of molecules
striking the surface per unit time. If they are going by the surface at a slower
average forward velocity, they strike the surface more frequently and we see a
higher pressure.
>
> Bernie
>
>
>
>
>> Homepage: http://www.flyrotary.com/
> >> Archive: http://lancaironline.net/lists/flyrotary/List.html
mfree1.gif
mfree1b.gif
mfree2.gif
|